Gradient descent(경사하강법)란 함수의 특정 위치에서 함수의 경사(기울기)를 구하고 그 반대 방향으로 이동하는 것을 반복함으로써 함수의 최소값을 찾아가는 알고리즘이다.
앞서 Gradient 벡터에서 살펴보았듯 Gradient를 사용하면 특정 지점에서 가장 기울기가 가파른 곳으로 향하는 벡터를 구할 수 있기 때문에 이 반대로 이동한다면 값이 줄어드는 원리를 사용하는 것이다.
https://devs0n.tistory.com/152
Gradient Vector
다음과 같은 다항식이 있을 때 $$ f(x, y)=x^2+2 x y+y^2 $$ Gradient 벡터는 각 항에 대한 편미분을 원소로 갖는 벡터의 형태를 가진다. $$ \nabla f(x, y)=\frac{\partial f(x, y)}{\partial x} \vec{i}+\frac{\partial f(x, y)}{\pa
devs0n.tistory.com
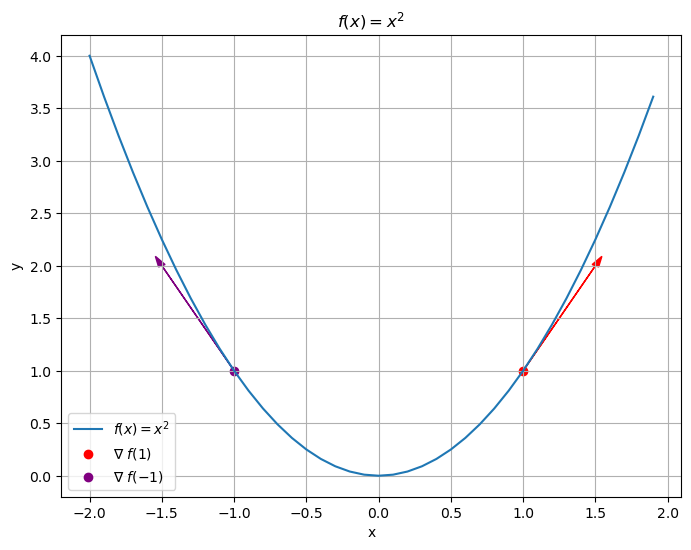
$ f(x) = x^2 $ 를 통해 gradient descent를 살펴보자.
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(8, 6))
# y = x^2 graph
x = np.arange(-2, 2, 0.1)
y = x**2
plt.plot(x, y, label="$f(x) = x^2$")
# (1,1)
# point
plt.scatter(1, 1, color="red", label="∇ $f(1)$")
# slope
plt.arrow(1.0, 1.0, 0.5, 1.0,
head_width=0.05, head_length=0.1,
fc="red", ec="red")
# (-1, 1)
# point
plt.scatter(-1, 1, color="purple", label="∇ $f(-1)$")
# slope
plt.arrow(-1.0, 1.0, -0.5, 1.0,
head_width=0.05, head_length=0.1,
fc="purple", ec="purple")
plt.title('$f(x) = x^2$')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
$ f(x) = x^2 $ 는 $ x=0 $ 을 기준으로 기울기가 변하는 것을 확인할 수 있고, 특정 지점에서 최소값으로 향하는 방향을 기울기 기준으로 확인할 수 있다.
- $ (1, 1) $ 지점에서 Gradient가 +2 값을 가지며, 그 반대 방향인 -x 방향으로 이동하면 y의 값이 작아진다.
- $ (-1, 1) $ 지점에서 Gradient가 -2 값을 가지며, 그 반대 방향인 +x 방향으로 이동하면 y의 값이 작아진다.

이러한 원리를 통해 아래와 같이 점진적으로 함수의 최소값을 찾아갈 수 있다.

하지만 한 step이 어떻게 되냐에 따라 최소값을 찾지 못하고 오히려 발산하거나 같은 좌표를 반복할 수 있다.

수식으로써 이를 확인해보자.
다음 좌표를 단순히 현재 좌표에서 gradient 뺀다면 아래와 같은 수식이 나온다.
$ x_{i+1} = x_i - \nabla f(x_{i}) $
$ f(x) = x^2 $ 라는 함수에서 초기 위치가 $ (1, 1) $ 인 경우에 위 수식을 기준으로 다음 x 좌표를 찾는다면 -1 이 나온다.
$ x_{2} = x_1 - \nabla f(x_{1}) = 1 - \nabla f(1) = 1 - 2 = -1 $
그리고 그 다음 x 좌표는 1이 나오게 된다.
$ x_{3} = x_2 - \nabla f(x_{2}) = -1 - \nabla f(-1) = -1 + 2 = 1 $
이를 계속 반복하면 x 좌표가 -1와 1을 반복하게 된다.
$ x_{4} = x_3 - \nabla f(x_{3}) = 1 - \nabla f(1) = 1 - 2 = -1 $
$ x_{5} = x_4 - \nabla f(x_{4}) = -1 - \nabla f(-1) = -1 + 2 = 1 $
$ ... $
이렇듯 이렇듯 단순히 현재 좌표에서 gradient를 빼면, 함수에 따라 gradient의 크기가 큰 경우가 있기 때문에 최소값을 제대로 찾을 수 없는 케이스도 있게된다.
그렇기 때문에 learning rate를 적용하여 최소값을 찾아 이동하는 정도를 조정해줘야한다.
$ x_{i+1} = x_i - \alpha \nabla f(x_{i}) $
이 $ \alpha $ 값에 따라 효율적으로 최소값을 찾아갈 수도 그렇지 않을 수도 있기 때문에 적절한 값을 찾는 튜닝이 필요하다.

또한 Gradient descent 사용 시, global 한 최소값이 아닌 local 최소값에 빠질 수도 있다.
이를 local minima 문제라고 하며 이를 해결하기 위한 방법 또한 있다. (이 포스팅에서는 다루진 않는다)
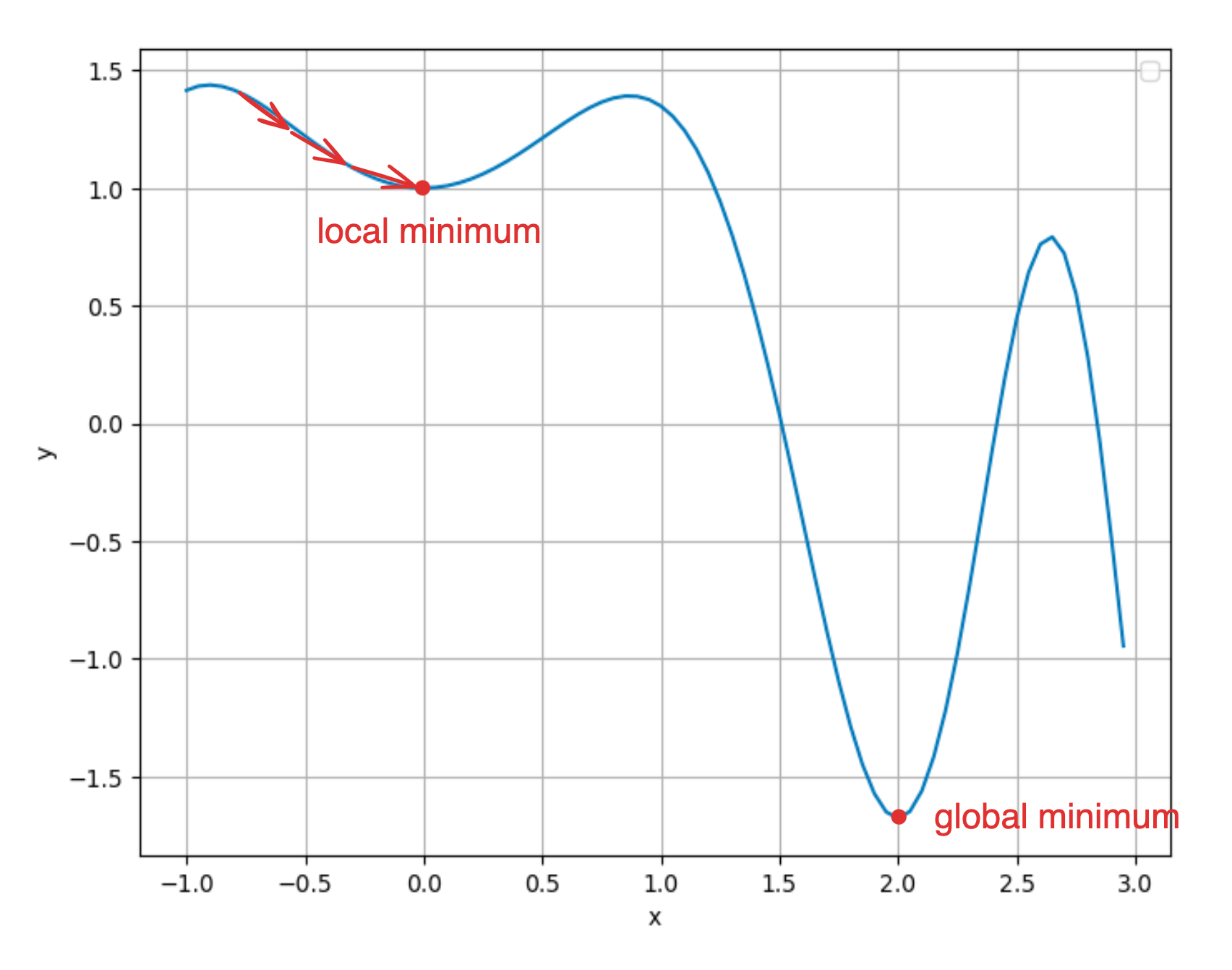
(같이 읽어보면 좋은 글 - Local Minima 문제에도 불구하고 딥러닝이 잘 되는 이유는?)
'Machine Learning' 카테고리의 다른 글
| ROC Curve (0) | 2024.05.23 |
|---|---|
| Classification task에서 Cross-Entropy (0) | 2024.05.18 |
| L1, L2 Regularization (0) | 2024.05.07 |
| Feature scaling 과 머신러닝 학습 (0) | 2024.04.26 |
| Gradient Vector (0) | 2024.02.19 |




댓글