[통계] Maximum Likelihood Estimation (MLE)
MLE는 딥러닝에 있어서 가장 기본이 되는 개념으로, 딥러닝 모델 자체가 결국 데이터를 일반화하는 분포를 찾기 위함이기에 MLE를 밑바탕으로 한다.
이번 포스팅에서는 MLE를 이해하기 위해 먼저 Likelihood에 대해 알아보고 MLE와 MLE가 딥러닝에서 어떻게 쓰이는지 알아보도록 하겠다.
Likelihood vs Probability
Likelihood(우도, 가능도)는 Probability(확률)과 헷갈리는 부분이 있다.
Probability
먼저 Probaility는 주어진(고정된) 확률분포가 있다고 했을 때, 관측하고자 하는 값이나 구간이 해당 확률분포 얼마만큼 나타날 수 있는가에 대한 값이다.
$P(확률변수 | 분포)$와 같이 나타낼 수 있다.
예를 들어 고정된 표준정규분포에서 확률변수 X가 1 이상일 확률은 아래와 같이 표현된다.
$$P(X > 1 | \mu=0, \sigma^{2} =1)$$

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = norm.pdf(x, 0, 1)
plt.plot(x, y, "b-")
plt.fill_between(x[66:], y[66:], alpha=0.5, color="red")
Likelihood
Likelihood는 Probability와는 반대로 고정된 샘플 데이터가 있을 때, 해당 데이터가 특정 확률분포에서 얼마나 나올법한지를 측정하는 값이다.
$L(분포 | 데이터)$와 같이 나타낼 수 있다.
예를 들어 아래와 같이 a, b라는 확률분포가 있을 때, X=1인 확률변수가 있다고 하자.
그럼 X는 a와 b 중에 어느 확률분포에서 나올 가능성이 더 높을까?

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
distribution_a = norm.pdf(x, 0, 1)
distribution_b = norm.pdf(x+1, 0, 1)
plt.plot(x, distribution_a, "b-", label="a")
plt.plot(x, distribution_b, "r-", label="b")
plt.plot([1]*20, np.linspace(0, 0.5, 20))
plt.legend()
X=1 일 때, 확률분포 a 에서의 값이 더 크기 때문에 X는 a에서 나올 가능성이 더 높다.

지금까지는 Likelihood의 intuition에 대해 설명했다.
정확한 Likelihood function는 다음과 같이 표현된다.
$$L(\theta | x) = \prod_{i=1}^{n} f(x_{i} | \theta)
= f(x_{1} | \theta) \cdot f(x_{2} | \theta) ... f(x_{n} | \theta)$$
여기서 $\theta$는 특정 분포를 만드는 파라미터라고 보면 된다. (gaussian 분포라면 $\mu$, $\sigma$가 될 수 있겠다)
위 수식을 보면 특정 파라미터 $\theta$ 를 통해 만들어진 분포에 대해 각 데이터 샘플을 넣은 값의 곱이다. (결합확률이기에 곱셈을 한다)
(표기에 따라 $L(\theta | x)$는 $P(x | \theta)$로도 표기된다 - 참고)
Maximum Likelihood Estimation (MLE)
MLE는 앞서 Likelihood의 예제처럼 고정된 샘플 데이터에 대해서 Likelihood를 통해 해당 데이터가 나올법한 가장 가능성있는 분포를 찾는 것이다.
앞서 Likelihood function은 아래와 같다고 하였다.
$$L(\theta | x) = \prod_{i=1}^{n} f(x_{i} | \theta)$$
MLE는 이 Likelihood를 최대화하는 $\theta$ 인 $\hat \theta$을 찾는 것이다.
$$ \hat \theta = \operatorname*{argmin}_\theta L(\theta | x) = \operatorname*{argmin}_\theta \prod_{i=1}^{n} f(x_{i} | \theta) $$
여기서 확률분포에 대해 $f(x_n | \theta)$의 값은 1보다 작으므로 데이터 샘플이 많은 경우 $L(\theta | x) = \prod_{i=1}^{n} f(x_{i} | \theta)$ 값은 매우 작아질 수 있어 컴퓨터로 계산 시 오류가 날 수도 있다.
그러므로 딥러닝에서는 log를 씌운 Log Likelihood를 주로 사용한다. (곱셈 -> 덧셈)
(log 함수는 단조 증가이므로 log를 씌워도 Likelihood의 대소관계가 바뀌지 않음)
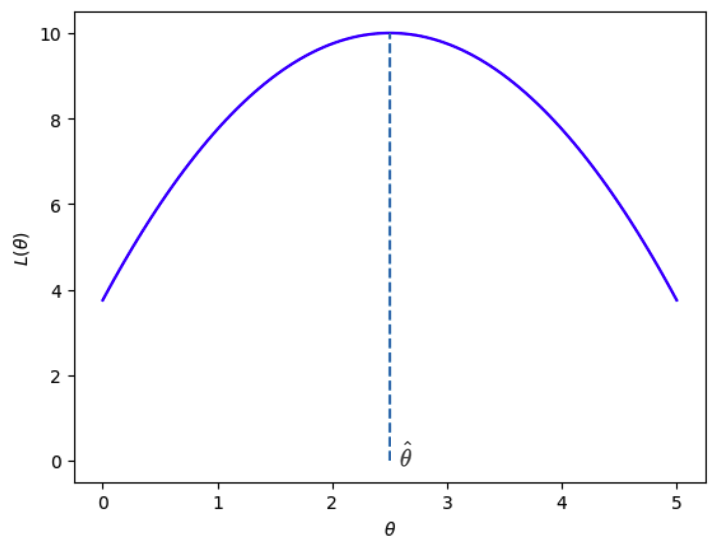
그럼 Likelihood가 최대가 되는 파라미터 $\theta$는 어떻게 구할 수 있을까?
쉽게 생각하면 $\theta$에 따른 Likehood function의 기울기가 0인 지점을 찾으면 된다.
$$ \frac{\partial L(\theta)}{\partial \theta} = 0 $$
딥러닝과 MLE
마지막으로 MLE가 딥러닝에서 어떻게 쓰이는지 알아보자.
사건의 결과가 2개인 베르누이 분포 $p^{x}(1-p)^{(1-x)}$ 를 Likelihood function으로 나타내면 아래와 같다.
$$ L(\theta) = \prod_{i=1}^{n} p^{x_i} (1-p)^{(1-x_i)} $$
여기에 log를 씌우면
$$ \log L(\theta) = \sum_{i=1}^{n} {x_i} \log p + {(1-x_i)} \log (1-p) $$
여기에 음수를 붙이면 Binary CrossEnropy와 수식이 동일해진다.
$$ - \log L(\theta) = - \sum_{i=1}^{n} \left ( {x_i} \log p + {(1-x_i)} \log (1-p) \right ) $$
$$BCE = - \sum \left ( {y} \log {\hat y} + {(1-y)} \log (1- \hat y) \right ) $$
즉, Binary CrossEntropy를 사용하는 것은 분류 모델에서 추정하는 데이터의 분포가 베르누이 분포를 따르고 있음을 가정한다는 것이다.
이렇듯 MLE는 모델이 데이터에 대해서 최적의 분포를 찾기위해서 사용되고 있다.
참고