[통계] 확률분포의 Expected Value & Variance
Expected Value (기대값)
확률이 없이 주어진 값에 대해 평균 값을 구하는 산술 평균과는 달리, ($\mu = \frac{1}{N} \sum_{i=1}^N x_i $)
확률분포의 기대값은 확률적 사건에 대해 평균을 구하기 때문에 확률을 고려해서 계산을 해야한다.
이산 확률 변수
이산 확률 변수에서의 기대값을 구하는 수식은 아래와 같다.
$$E[X] = \sum_{i=1}^{N} x_{i}P(x_{i})$$
- $x_{i}$: 확률 변수가 가질 수 있는 값
- $P(x_{i})$: 해당 값이 나올 확률 - 확률 질량 함수 (probability mass function)
예시 - 주사위
정육면체 주사위의 경우 각 면이 나올 확률은 $\frac{1}{6}$로 동일하다.
그러면 주사위에 대한 기대값은 아래와 같이 구할 수 있다.
$$ 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6} = 3.5 $$
(이는 무한대로 주사위 던지기를 하였을 때의 산술 평균과 동일하다)
연속 확률 변수
연속 확률 변수에서의 기대값을 구하는 수식은 아래와 같다.
$$E[X] = \int_{-\infty}^{\infty} x f(x) \,dx$$
- $x$: 확률 변수가 가질 수 있는 값
- $f(x)$: 확률 밀도함수(probability density function)
확률밀도함수 P(x) = 2x, if 0<= x <=1. 0, otherwise
예시 - 표준 정규분포
표준 정규분포는 평균이 0이고 분산이 1인 정규분포로 연속 확률 분포이다.
표준 정규분포의 확률 밀도함수는 $f(x) = \frac{1}{\sqrt{2 \pi}} e^{\frac{x^2}{2}}$ 이다.
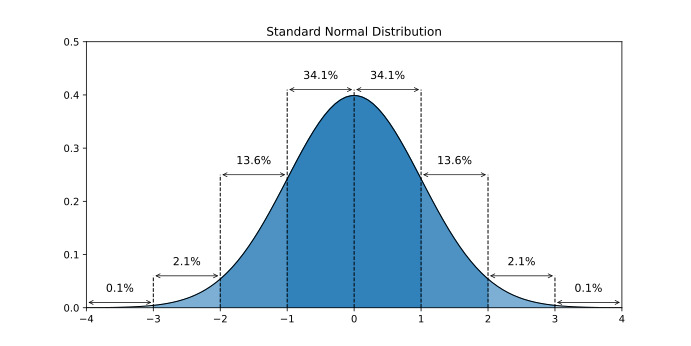
이 함수는 보다시피 0을 기준으로 좌우대칭을 이루고 있기 때문에 $x$ 가 $-\infty \sim 0$일 때와 $0 \sim \infty$일 때의 $f(x)$의 적분값은 동일하다.
그러므로 표준 정규분포의 기대값은 계산 필요없이 0임을 알 수 있다.
$E[X] = \int_{-\infty}^{0} x f(x) \,dx + \int_{0}^{\infty} x f(x) \,dx = \int_{0}^{\infty} -x f(x) \,dx + \int_{0}^{\infty} x f(x) \,dx$
Variance (분산)
분산은 평균으로부터 값들의 퍼진 정도를 나타내는 값으로 확률분포 상으로는 기대값이 평균의 역할을 하기 때문에 기대값으로부터 퍼진 정도를 구한다고 보면 된다.
기대값으로부터 퍼진 정도를 구하기 위해 확률 변수 값에서 기대값을 뺀 값을 사용한다.
이산 확률 변수
이산 확률 변수에서의 분산을 구하는 수식은 아래와 같다.
$$V[X] = \sum_{i=1}^{N} (x_i - E[X])^2 P(x_{i})$$
이 수식은 다음과 같이 보다 단순하게 표현될 수 있다.
$$V[X] = E[X^{2}] - E[X]^{2}$$
수식 풀이
$$
V[X] = \sum_{i=1}^{N} (x_{i}^{2}P(x_{i}) -2E[X]x_{i}P(x_{i}) + E[X]^{2}P(x_{i})) \\
= \sum_{i=1}^{N} x_{i}^{2}P(x_{i}) -2E[X] \sum_{i=1}^{N} x_{i}P(x_{i}) + E[X]^{2} \sum_{i=1}^{N} P(x_{i})
$$
여기서
- $\sum_{i=1}^{N} x_{i}^{2}P(x_{i}) = E[X^{2}]$
- $\sum_{i=1}^{N} x_{i}P(x_{i}) = E[X]$
- $\sum_{i=1}^{N} P(x_{i}) = 1$ (확률은 모두 합하면 1이기 때문에)
그러므로
$$ V[X] = E[X^{2}]- 2E[X]^{2} + E[X]^{2} = E[X^{2}] - E[X]^{2} $$
연속 확률 변수
이산 확률 변수에서의 분산을 구하는 수식은 아래와 같다.
$$V[X] = \int_{-\infty}^{\infty} (x - E[X])^2 f(x) \, dx$$
그리고 이 역시 다음과 같이 보다 단순하게 표현될 수 있다.
$$V[X] = E[X^{2}] - E[X]^{2}$$
참고
https://infograph.tistory.com/191
https://blog.naver.com/yunjh7024/220829584385
https://blog.naver.com/yunjh7024/220823945749