이번 포스팅에서는 image generative model의 기본 모델인 Variational Auto Encoder(이하 VAE)에 대해 정리하도록 한다.
단순하게 VAE의 구조와 관련 수식을 정리하는 것이 아니라 왜 VAE가 Encoder와 Decoder의 구조를 가지게 되었고 수식은 어떻게 나오게 되었는지 논리적인 흐름을 따라가고자 한다.
First approach
먼저 최초의 동기는 저차원의 latent space에서 샘플링 된 latent variable $z$를 통해 고차원의 이미지 $x$를 생성하고자하는 것이다
저차원의 latent space는 고차원의 이미지에 대한 feature를 다룬다.
예를 들어 사람 얼굴 이미지를 생성하는 것이 목적이라면 latent space의 각 차원은 사람 얼굴에 대한 feature인 고개 각도, 얼굴 길이, 눈의 모양 등을 다룰 수 있을 것이다.
그렇기 때문에 latent space에서 feature를 적절하게 학습했다면, latent space에서 샘플링한 z를 통해서 다양한 이미지를 생성할 수 있게될 것이다.
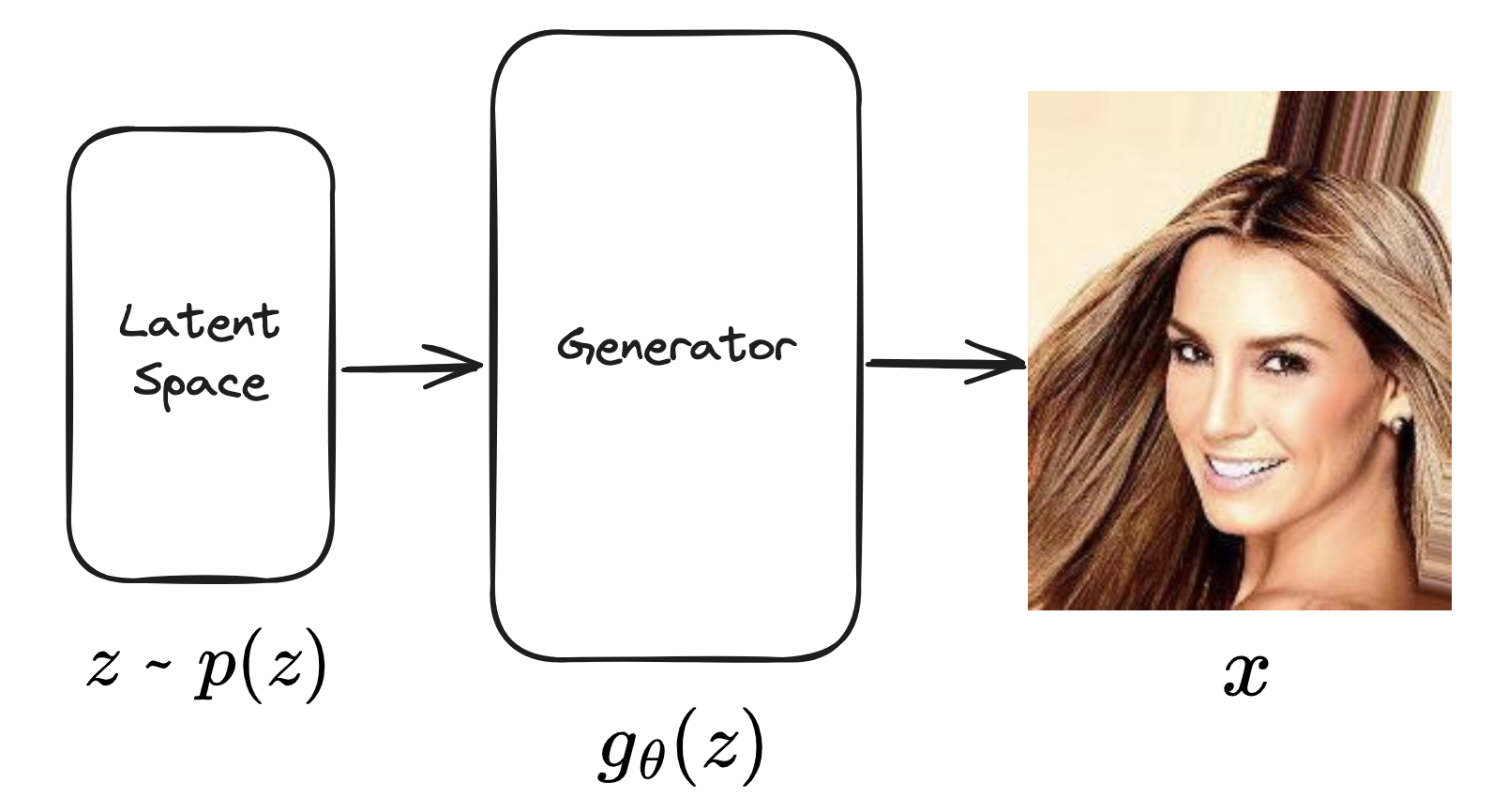
(VAE의 구조를 이미 알고 있다면 Decoder 형태와 동일하다. 하지만 아직은 Decoder에서의 가정이 들어가지 않았으므로 엄밀하게는 Decoder라고 볼 순 없다.)
이미지인 x에 대한 분포 $p(x)$를 알게된다면 궁극적으로는 해당 분포를 통해 이미지를 가져올 수 있게될 것이다.
이를 수식으로 나타내면 다음과 같다.
$p(x)= \int p(x,z) dz \\
\qquad = \int p(x|z) p(z) dz \qquad (\because p(x,z) = p(x|z)p(z)) \\
\qquad = \int p(x|g_{\theta}(z)) p(z) dz) \qquad (\because p_{\theta}(x | z) = p(x | g_{\theta}(z)) \\
\qquad \approx \sum_{i} p(x|g_{\theta}(z_i)) p(z_{i}) \\
\qquad \approx E_{q(z)}[p(x|g_{\theta}(z))] $
MLE(maximum likelihood estimation) 관점에서 본다면 $p(x)$에 대한 likelihood를 최대화하는 Generator의 파라미터 $\theta$를 찾는 것이다.
$p(x)$에 대한 likelihood function은 위 수식을 통해 다음과 같이 정리된다.
$$L(\theta) = \prod_{i} p(x_{i} | g_{\theta}(z_{i})$$
$$\rightarrow l(\theta) = \sum_{i} \log {p(x_{i} | g_{\theta}(z_{i}))}$$
이제 $p(x | g_{\theta}(z))$가 정규분포를 따른다고 하면 결과적으로 MSE를 구하는 것과 동일해지며,
이는 $x_{i}$와 $g_{\theta}(z_{i})$가 최대한 같아져야한다는 것이다.
하지만 단순히 값만 같아지려고 하는 경우에는 이미지에 대한 semantics를 반영하지 못한다.

위 이미지에서 (a)는 MNIST 데이터셋에 있는 이미지이고 (b)와 (c)가 생성된 이미지이다.
- (b): (a)와 이미지는 거의 같지만 숫자의 좌하단 부분이 짤려있다.
- (c): (a)의 이미지 형태는 그대로 갖지만 픽셀이 오른쪽으로 밀려있다.
(b), (c)에 대해서 (a)와의 MSE를 구하면 $MSE(a, b) < MSE(a, c)$ 와 같은 결과를 갖는데,
MSE 수치로는 숫자 2의 의미가 깎여버린 (b)가 숫자 2라는 의미지를 더 잘 표현한 (c)보다 픽셀의 차이가 적다는 것이다.
➡️ 이는 단순히 $p(x)$에 대해 MLE를 사용하면 이미지에 대한 semantics를 반영할 수 없다는 것을 의미한다.
Second approach
그렇기 때문에 보다 의미있는 이미지를 생성하기 위해서 다른 접근을 취해야한다.
그 접근 방식은 $z$에서 바로 $x$를 구하는 것이 아니라
$x$를 잘 표현할 수 있는 $z$를 샘플링하기 위해 $p(z|x)$를 구하고, $p(z|x)$에서 샘플링한 $z$를 통해 $x$를 구하는 것이다.

하지만 $p(z|x)$를 직접적으로 구하기 쉽지 않기에 Variational Inference를 활용한다.
(상대적으로 더 구하기 쉬운 다른 분포를 $p(z|x)$ 대신에 사용한다는 것이다)
이를 위해 Encoder 부분을 추가하도록 한다.
Encoder를 통해 $p(z|x)$를 $q_{\phi}(z|x)$로 근사한다.
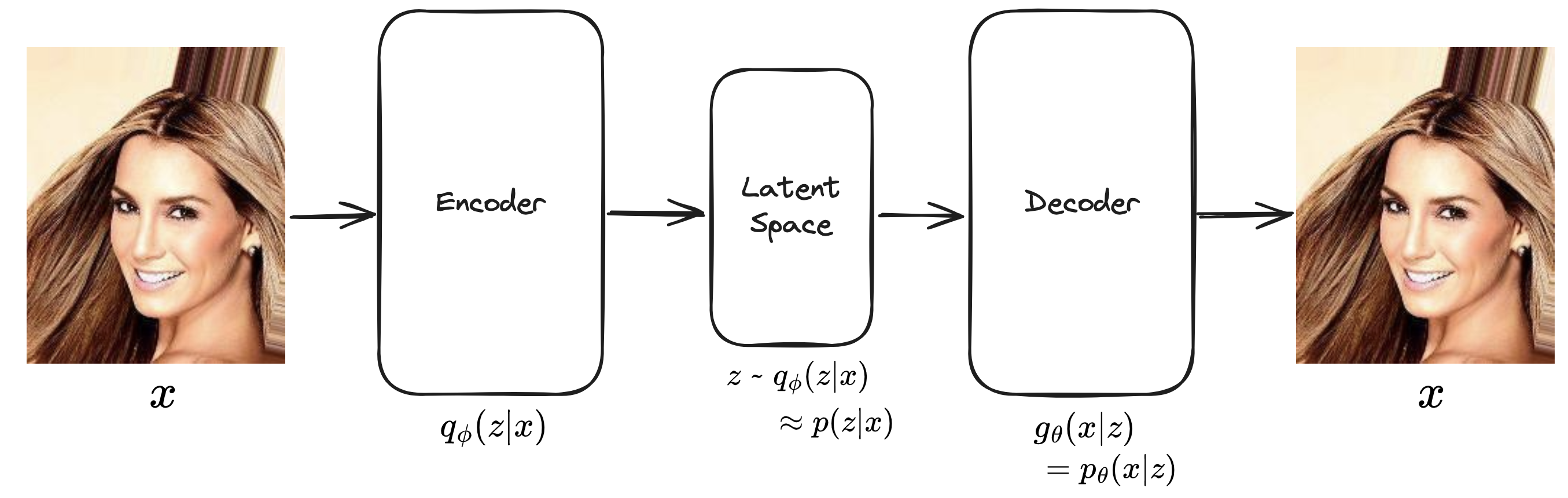
그러면 $p(x)$에 대한 수식을 $q_{\phi}(z|x)$를 사용한 수식으로 다시 풀어보자.
$\log{p(x)} = \log{p(x)} \int q_{\phi}(z|x)dz \qquad$ (∵ z에 대한 확률 분포를 모든 z에 대해 적분하면 1)
$\qquad = \int q_{\phi}(z|x) \log{p(x)} dz$
$\qquad = \int q_{\phi}(z|x) \log{ \frac{p(x|z)p(z)}{p(z|x)}} dz \qquad(\because \ \text{Bayes' rule})$
$\qquad = \int q_{\phi}(z|x) \log { \left ( \frac{p(x|z)p(z)}{p(z|x)} \frac{q_{\phi}(z|x)}{q_{\phi}(z|x)} \right ) }$
$\qquad = \int q_{\phi}(z|x) \log {p(x|z)}dz - \int q_{\phi}(z|x) \log { \frac{q_{\phi}(z|x)}{p(z)} }dz + \int q_{\phi}(z|x) \log { \frac{q_{\phi}(z|x)}{p(z|x)} }dz $
$\qquad = \mathbb{E}_{q_{\phi}(z|x)} \log{ p(x|z) } - D_{KL}(q_{\phi}(z|x) || p(z)) + D_{KL}(q_{\phi}(z|x) || p(z|x))$
최종적으로 $log(p(x))$는 3개의 term이 남게된다.
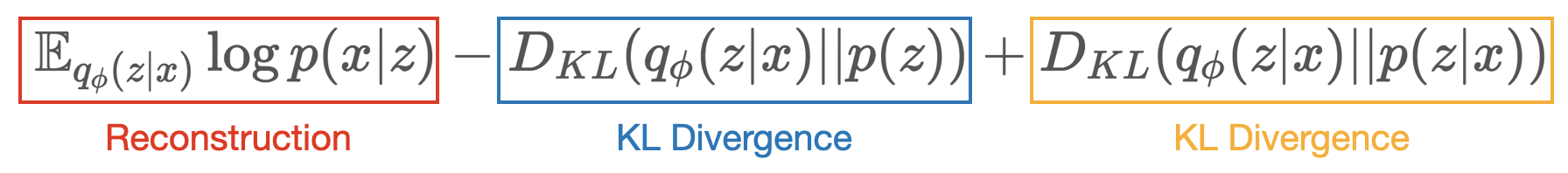
여기서 마지막 KL Divergence term은 $p(z|x)$로 인해 구할 수 없다.
마지막 term은 구할 순 없지만 KL Divergence 값은 0 이상의 값을 갖기 때문에 $\log{p(x)}$에 대해 lower bound를 만들 수 있다.
$$\log{p(x)} >= \mathbb{E}_{q_{\phi}(z|x)} \log{ p(x|z) } - D_{KL}(q_{\phi}(z|x) || p(z))$$
이 $\log{p(x)}$의 lower bound를 Evidence of Lower Bound, ELBO라고 한다.

$$ \log{p(x)} = ELBO(\phi) + D_{KL}(q_{\phi}(z|x) || p(z|x)) $$
이 수식을 좀 더 살펴보면, $x$는 우리가 갖고 있는 유한한 이미지 데이터셋이므로 $ \log{p(x)} $의 경우 그 값은 몰라도 고정된 값으로 볼 수 있다.
그러면 $ELBO(\phi)$ 값이 커지면 반대로 $D_{KL}(q_{\phi}(z|x) || p(z|x))$ 값은 작아지게 된다.

$D_{KL}(q_{\phi}(z|x) || p(z|x))$가 작아진다는 것은 $q_{\phi}(z|x)$가 $p(z|x)$를 더 잘 근사할 수 있게 되는 것이므로,
$ELBO(\phi)$를 최대화 하면 $q_{\phi}(z|x)$가 $p(z|x)$를 더 잘 근사할 수 있게 된다.
이는 Encoder를 통해 구하기 힘든 $p(z|x)$를 근사해보자는 동기와도 일치한다.
이제 새로운 방식의 학습 목표는 이 $ELBO(\phi)$를 최대화하는 것이 된다.
ELBO term
ELBO term은 KL Divergence와 Reconsturction term으로 구성된다.

- $D_{KL}(q_{\phi}(z|x) || p(z))$ - KL Divergence term
- $q_{\phi}(z|x)$와 $p(z)$의 분포 차이에 대한 값으로,
음수 값이기 때문에 ELBO를 최대화하기 위해서는 이 값이 최소화되어야 한다. - 이 term을 통해 $q_{\phi}(z|x)$가 $p(z)$와 유사해지도록 한다.
- VAE 논문에서 $p(z)$를 표준정규분포라고 가정했을 때의 KL Divergence term을 구하는 수식에 대한 유도를 정리를 해두었다.
- $q_{\phi}(z|x)$와 $p(z)$의 분포 차이에 대한 값으로,

- $\mathbb{E}_{q_{\phi}(z|x)} \log{ p(x|z) }$ - Reconstruction term
- $q_{\phi}(z|x)$ 분포에서 샘플링한 $z$에 대해서 $p(x|z)$ 분포의 기대값으로,
결국 VAE에서 $x$가 입력으로 주어졌을 때 출력으로 그대로 $x$를 얼마나 잘 출력하는지에 대한 값이다.- 가정하는 $x$의 분포에 따라 MSE나 CrossEntropy를 사용한다.
- 양수 값이기 때문에 ELBO를 최대화하기 위해서는 이 값이 커질수록 좋다.
- $z$는 $q_{\phi}(z|x)$ 분포에서 샘플링 된 값이다.
샘플링은 미분이 불가능하기 때문에 backpropagation을 통해 학습할 수 없다.
이를 Reparameterization trick을 통해서 미분 가능하게 풀 수 있다.
- $q_{\phi}(z|x)$ 분포에서 샘플링한 $z$에 대해서 $p(x|z)$ 분포의 기대값으로,
Reparameterization trick
Encoder에서는 $z$를 샘플링하기 위한 latent space의 $q_{\phi}(z|x)$의 평균과 분산을 출력한다.
(그리고 주로 이를 표준정규분포가 되도록 한다)
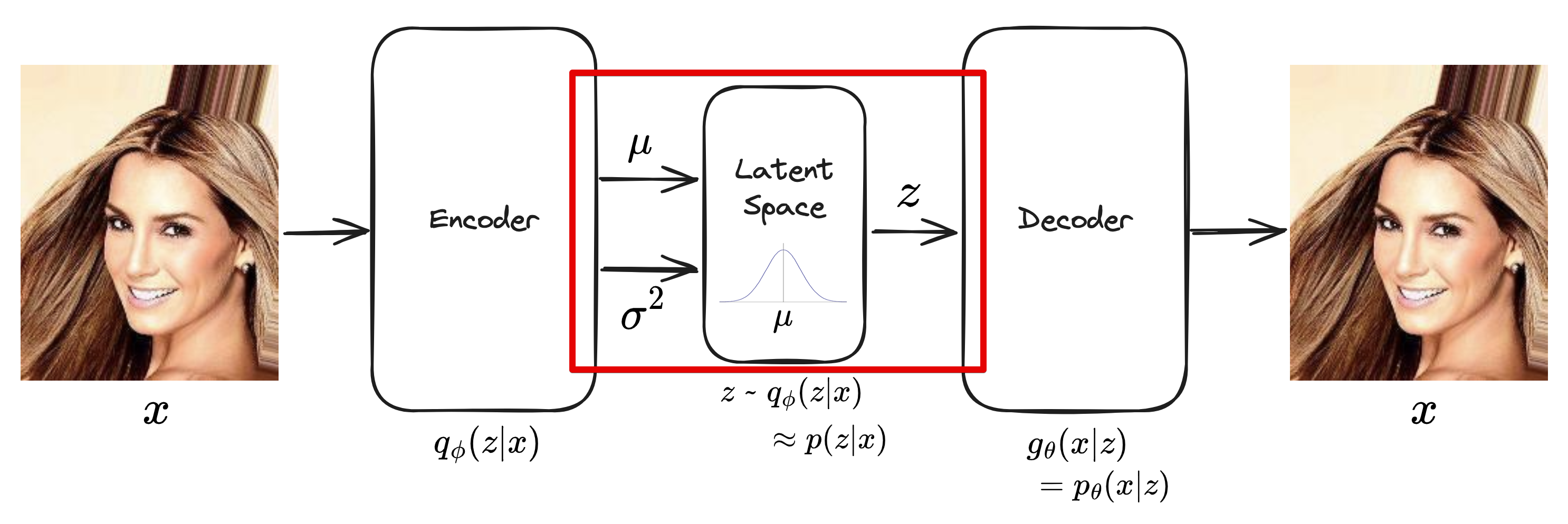
Reparameterization trick는 분포로 부터 직접 샘플링하는 것이 아니라,
샘플링할 대상을 외부의 파라미터($\epsilon$)로 두고 이를 평균($\mu$)과 표준편차($\sigma$)을 이용한 식으로 바꿔 동일한 결과를 만들도록 하는 것이다.
$$z = q_{\phi}(z|x)$$
$$\rightarrow z = \mu + \sigma \odot \epsilon , \text{where} \ \epsilon \sim N(0, I)$$

Reparameterization trick을 통해 backpropagation이 가능한 계산을 할 수 있게된다.
지금까지 VAE 이론적인 부분을 살펴보았다.
다음으로는 VAE를 직접 코드로 구현해보도록 하겠다.
참고
- 논문
- 영상
'Machine Learning > Paper' 카테고리의 다른 글
| [논문 구현] Auto-Encoding Variational Bayes (Varitional Auto Encoder) (0) | 2024.08.05 |
|---|---|
| [논문 리뷰] Deep Residual Learning for Image Recognition (0) | 2024.07.01 |


댓글